关于Matrix
我们先看看chatGpt是如何介绍矩阵的。
矩阵是数学中的一个概念,它是由数字按照矩形排列而成的矩形阵列。矩阵由行和列组成,行表示矩阵的水平方向,列表示矩阵的垂直方向。
一个矩阵可以用以下形式表示:
A = [a11, a12, a13, ..., a1n]
[a21, a22, a23, ..., a2n]
[a31, a32, a33, ..., a3n]
...
[am1, am2, am3, ..., amn]其中,a11, a12, a13, ..., a1n 表示第一行的元素,a21, a22, a23, ..., a2n 表示第二行的元素,以此类推,am1, am2, am3, ..., amn 表示第 m 行的元素。
矩阵的大小由行数和列数决定,如果一个矩阵有 m 行和 n 列,我们称其为 m×n 的矩阵。
矩阵在数学和计算机科学中有广泛的应用,例如线性代数、图形学、机器学习等领域。矩阵可以进行加法、减法、乘法等运算,还可以表示向量、线性方程组、线性变换等概念。
在 CSS 中,矩阵也被用于表示 2D 变换效果,如平移、缩放、旋转和错切等。通过矩阵的乘法运算,可以将多个变换效果组合在一起,实现复杂的变换效果。
CSS3 transform的matrix()
transform: matrix(a,b,c,d,e,f);实际上,这6参数,对应的矩阵就是:
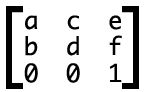
注意书写方向是竖着的。
假如矩阵要变化,例如偏移,旋转或者变形或者其他的中心点是xy,那么矩阵变化如下
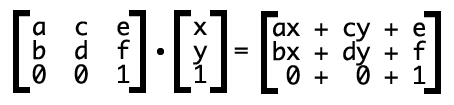
其中,x, y表示转换元素的所有坐标(变量)了。那后面的ax+cy+e怎么来的呢? 很简单,33矩阵每一行的第1个值与后面13的第1个值相乘,第2个值与第2个相乘,第3个与第3个,然后相加,如下图同色标注:
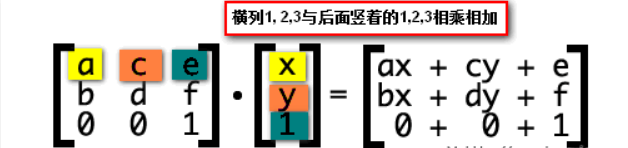
那ax+cy+e的意义是什么?
ax+cy+e为变换后的水平坐标,
bx+dy+f表示变换后的垂直位置。
矩阵偏移
关于偏移,假如是如下矩阵
transform: matrix(1, 0, 0, 1, 60, 60); /* a=1, b=0, c=0, d=1, e=60, f=60 */现在,我们根据这个矩阵偏移元素的中心点,假设是(0, 0),即x=0, y=0。
于是,变换后的
x坐标就是ax+cy+e = 10+00+60 =60,
y坐标就是bx+dy+f = 00+10+60 =60.
于是,中心点坐标从(0, 0)变成了→(60, 60)。
也就是相当于
transform: translate(60px, 60px);注意:translate, rotate等方法都是需要单位的,而matrix方法e, f参数的单位可以省略。
矩阵缩放(scale)
发现没,matrix(1, 0, 0, 1, 60, 60);的元素比例与原来一样,1:1, 而这几个参数中,有两个1,
没错,这两个1就是缩放相关的参数。
其中,第一个缩放x轴,第二个缩放y轴。
用公式就很明白了,假设比例是s,则有matrix(s, 0, 0, s, 0, 0);,于是,套用公式,就有:
x' = ax+cy+e = sx+0y+0 = s*x;
y' = bx+dy+f = 0x+sy+0 = s*y;
也就是
matrix(sx, 0, 0, sy, 0, 0);,等同于
scale(sx, sy);矩阵旋转(rotate)
旋转相比前面两个要更高级些,要用到三角函数。
方法以及参数使用如下(假设角度为θ):
matrix(cosθ,sinθ,-sinθ,cosθ,0,0)结合矩阵公式,就有:
x' = x*cosθ-y*sinθ+0 = x*cosθ-y*sinθ
y' = x*sinθ+y*cosθ+0 = x*sinθ+y*cosθ假如
transform:rotate(30deg);转换成矩阵就是
transform: matrix(0.866025,0.500000,-0.500000,0.866025,0,0);矩阵拉伸(skew)
拉伸也用到了三角函数,不过是tanθ,而且,其至于b, c两个参数相关,书写如下(注意y轴倾斜角度在前):
matrix(1,tan(θy),tan(θx),1,0,0)对应公式如下:
x' = x+y*tan(θx)+0 = x+y*tan(θx)
y' = x*tan(θy)+y+0 = x*tan(θy)+y对应于skew(θx + "deg",θy+ "deg")这种写法。
其中,θx表示x轴倾斜的角度,θy表示y轴,两者并无关联。
矩阵matrix实现镜像渐变
镜像主要是指transform里面其他属性实现不了的功能,轴围绕的那个点就是CSS3中transform变换的中心点, 因为该轴永远经过原点,因此,任意对称轴都可以用y = k * x表示。则matrix表示就是:
matrix((1-k*k) / (1+k*k), 2k / (1 + k*k), 2k / (1 + k*k), (k*k - 1) / (1+k*k), 0, 0)这个如何得到的呢?
一是垂直,二是中心点在轴线上,因此有:
(y-y') / (x - x') = -1/ k → ky-ky' = -x+x'
(x + x') / 2 * k = (y + y')/2 → kx+kx' = y+y'很简单的,把x'和y'提出来,就有:
x' = (1-k*k)/(k*k+1) *x + 2k/(k*k+1) *y;
y' = 2k/(k*k+1) *x + (k*k-1)/(k*k+1) *y;再结合矩阵公式:
x' = ax+cy+e;
y' = bx+dy+f;我们就可以得到:
a = (1-k*k)/(k*k+1);
b = 2k/(k*k+1);
c = 2k/(k*k+1);
d = (k*k-1)/(k*k+1);也就是上面matrix方法中的参数值啦!
3D变换中的矩阵
3D变换虽然只比2D多了一个D,但是复杂程度不只多了一个。从二维到三维,是从4到9;而在矩阵里头是从33变成44, 9到16了。
其实,本质上很多东西都与2D一致的,只是复杂度不一样而已。这里就举一个简单的3D缩放变换的例子。
transform: matrix3d(sx, 0, 0, 0, 0, sy, 0, 0, 0, 0, sz, 0, 0, 0, 0, 1)psd.js里面的字体矩阵旋转
psd.js解析的字体如下:
transform: {
tx: 243.2087255915381,
ty: 662.7336218363249,
xx: 0.3848003848003848,
xy: 0,
yx: 0,
yy: 0.38469353200135453,
}要将这些属性值转换为 CSS 中的 matrix,可以按照以下方式进行计算:
const transform = {
tx: 243.2087255915381,
ty: 662.7336218363249,
xx: 0.3848003848003848,
xy: 0,
yx: 0,
yy: 0.38469353200135453,
};
const matrixValue = `matrix(${transform.xx}, ${transform.xy}, ${transform.yx}, ${transform.yy}, ${transform.tx}, ${transform.ty})`;
console.log(matrixValue);在上面的代码中,我们使用 transform 对象中的属性值构建了 matrix 字符串。${transform.xx} 表示水平方向上的缩放比例,${transform.xy} 表示水平方向上的错切值,${transform.yx} 表示垂直方向上的错切值,${transform.yy} 表示垂直方向上的缩放比例,${transform.tx} 表示水平方向上的平移量,${transform.ty} 表示垂直方向上的平移量。